三菱着手开发全新S-AWC四驱系统 将引入电动机驱动

Grade da Terra. As linhas verticais de polo a polo s?o linhas de constante longitude, ou meridianos. Os círculos paralelos ao equador s?o linhas de constante latitude, ou paralelos. A grade mostra a latitude e a longitude dos pontos na superfície. Neste exemplo, os meridianos est?o espa?ados a intervalos de 6° e os paralelos a intervalos de 4°.

百度 让欧蓝德在保证出色动力性的同时，燃烧更充分，进一步降低油耗，我的实际体验的是车型，同样是城市正常驾驶，油量的下降速度明显比同级一些车型控制的更好。

Em geografia, latitude é uma coordenada que especifica a posi??o norte–sul de um ponto na superfície da Terra ou de outro corpo celeste. A latitude é dada como um angulo que varia de ?90° no polo sul a 90° no polo norte, com 0° no Equador. Linhas de latitude constante, ou paralelos, correm de leste a oeste como círculos paralelos ao equador. Latitude e longitude s?o usadas juntas como um par de coordenadas para especificar uma localiza??o na superfície da Terra.

Por si só, o termo "latitude" normalmente se refere à latitude geodésica, conforme definido abaixo. Resumidamente, a latitude geodésica de um ponto é o angulo formado entre o vetor perpendicular (ou normal) à superfície elipsoidal a partir do ponto e o plano do equador.

Contexto

Dois níveis de abstra??o s?o empregados nas defini??es de latitude e longitude. No primeiro passo, a superfície física é modelada pelo geoide, uma superfície que se aproxima do nível médio do mar sobre os oceanos e sua continua??o sob as massas terrestres. O segundo passo é aproximar o geoide por uma superfície de referência matematicamente mais simples. A escolha mais simples para a superfície de referência é uma esfera, mas o geoide é mais precisamente modelado por um elipsoide de revolu??o. As defini??es de latitude e longitude em tais superfícies de referência s?o detalhadas nas se??es seguintes. Linhas de latitude e longitude constantes juntas constituem uma grade na superfície de referência. A latitude de um ponto na superfície real é aquela do ponto correspondente na superfície de referência, a correspondência sendo ao longo da normal à superfície de referência, que passa pelo ponto na superfície física. Latitude e longitude, juntamente com alguma especifica??o de altura, constituem um sistema de coordenadas geográficas conforme definido na especifica??o da norma ISO 19111.

Como existem muitos elipsoides de referência diferentes, a latitude precisa de uma característica na superfície n?o é única: isso é destacado na norma ISO, que afirma que "sem a especifica??o completa do sistema de referência de coordenadas, as coordenadas (ou seja, latitude e longitude) s?o, na melhor das hipóteses, ambíguas e, na pior, sem sentido". Isso é de grande importancia em aplica??es precisas, como o Sistema de Posicionamento Global (GPS), mas no uso comum, onde n?o é necessária alta precis?o, o elipsoide de referência geralmente n?o é declarado.

Em textos em inglês, o angulo de latitude, definido abaixo, é geralmente denotado pela letra grega minúscula phi (? ou φ). é medido em graus, minutos e segundos ou graus decimais, ao norte ou ao sul do equador. Para fins de navega??o, as posi??es s?o dadas em graus e minutos decimais. Por exemplo, o farol de The Needles está a 50°39.734′ N 001°35.500′ W.

Este artigo relaciona-se a sistemas de coordenadas para a Terra: ele pode ser adaptado para cobrir a Lua, planetas e outros objetos celestes (latitude planetográfica).

Para um breve histórico, veja História da latitude.

Determina??o

Mais informa??es: Navega??o celestial § Latitude

Na navega??o celestial, a latitude é determinada pelo método da altura do meridiano. Medi??es mais precisas de latitude requerem uma compreens?o do campo gravitacional da Terra, seja para configurar teodolitos ou para determinar as órbitas dos satélites GPS. O estudo da forma da Terra juntamente com seu campo gravitacional é a ciência da geodesia.

Latitude na esfera

Uma vista em perspectiva da Terra mostrando como latitude ($\phi$) e longitude ($\lambda$) s?o definidas em um modelo esférico. O espa?amento da grade é de 10 graus.

A grade na esfera

A grade é formada pelas linhas de latitude constante e longitude constante, que s?o construídas com referência ao eixo de rota??o da Terra. Os pontos de referência primários s?o os polos onde o eixo de rota??o da Terra intersecta a superfície de referência. Planos que contêm o eixo de rota??o intersectam a superfície nos meridianos; e o angulo entre qualquer plano meridiano e aquele através de Greenwich (o Meridiano Principal) define a longitude: meridianos s?o linhas de longitude constante. O plano através do centro da Terra e perpendicular ao eixo de rota??o intersecta a superfície em um grande círculo chamado Equador. Planos paralelos ao plano equatorial intersectam a superfície em círculos de latitude constante; esses s?o os paralelos. O Equador tem latitude de 0°, o Polo Norte tem latitude de 90° Norte (escrito 90° N ou +90°), e o Polo Sul tem latitude de 90° Sul (escrito 90° S ou ?90°). A latitude de um ponto arbitrário é o angulo entre o plano equatorial e o normal à superfície nesse ponto: o normal à superfície da esfera está ao longo do vetor radial.

A latitude, conforme definida desta forma para a esfera, é frequentemente chamada de latitude esférica, para evitar ambiguidades com a latitude geodésica e as latitudes auxiliares definidas nas se??es subsequentes deste artigo.

Latitudes nomeadas na Terra

A orienta??o da Terra no solstício de dezembro

Além do equador, outros quatro paralelos s?o significativos:

Círculo Polar ártico	66° 34′ (66.57°) N
Trópico de Cancer	23° 26′ (23.43°) N
Trópico de Capricórnio	23° 26′ (23.43°) S
Círculo Polar Antártico	66° 34′ (66.57°) S

O plano da órbita da Terra ao redor do Sol é chamado de eclíptica, e o plano perpendicular ao eixo de rota??o da Terra é o plano equatorial. O angulo entre a eclíptica e o plano equatorial é chamado de inclina??o axial, obliquidade ou inclina??o da eclíptica, e é convencionalmente denotado por i. A latitude dos círculos tropicais é igual a i e a latitude dos círculos polares é seu complemento (90° - i). O eixo de rota??o varia lentamente ao longo do tempo e os valores fornecidos aqui s?o para a época atual. A varia??o do tempo é discutida mais detalhadamente no artigo sobre inclina??o axial.

A figura mostra a geometria de uma sec??o transversal do plano perpendicular à eclíptica e através dos centros da Terra e do Sol no solstício de dezembro, quando o Sol está diretamente sobre algum ponto do Trópico de Capricórnio. As latitudes polares sul abaixo do Círculo Polar Antártico est?o sob luz do dia, enquanto as latitudes polares norte acima do Círculo Polar ártico est?o na noite. A situa??o é invertida no solstício de junho, quando o Sol está diretamente sobre o Trópico de Cancer. Apenas nas latitudes entre os dois trópicos é possível que o Sol esteja diretamente acima (no zênite).

Em proje??es de mapas n?o há uma regra universal sobre como os meridianos e paralelos devem aparecer. Os exemplos abaixo mostram os paralelos nomeados (como linhas vermelhas) na proje??o de Mercator comumente usada e na proje??o de Mercator Transversa. Na primeira, os paralelos s?o horizontais e os meridianos s?o verticais, enquanto na última n?o há rela??o exata entre paralelos e meridianos com horizontais e verticais: ambos s?o curvas complicadas.

	Mercator Normal		Mercator Transversa
		\

Latitude no elipsoide

Elipsoides

Ver artigo principal: Elipsoide de revolu??o

Em 1687, Isaac Newton publicou o Philosophi? Naturalis Principia Mathematica, no qual ele provou que um corpo fluido auto-gravitante em rota??o em equilíbrio assume a forma de um elipsoide oblato. (Este artigo usa o termo elipsoide em preferência ao termo mais antigo esferoide.) O resultado de Newton foi confirmado por medi??es geodésicas no século XVIII. (Veja Arco de meridiano.) Um elipsoide oblato é a superfície tridimensional gerada pela rota??o de uma elipse em torno de seu eixo mais curto (eixo menor). "Elipsoide oblato de revolu??o" é abreviado para 'elipsoide' no restante deste artigo. (Elipsoides que n?o possuem um eixo de simetria s?o denominados triaxiais.)

Muitos elipsoides de referência diferentes foram usados na história da geodesia. Antes dos satélites, eles foram desenvolvidos para fornecer um bom ajuste ao geoide sobre a área limitada de um levantamento, mas, com o advento do GPS, tornou-se natural usar elipsoides de referência (como o WGS84) com o centro no centro de massa da Terra e eixo menor alinhado com o eixo de rota??o da Terra. Esses elipsoides geocêntricos geralmente est?o dentro de 100 m (330 ft) do geoide. Como a latitude é definida em rela??o a um elipsoide, a posi??o de um determinado ponto é diferente em cada elipsoide: n?o se pode especificar exatamente a latitude e longitude de uma característica geográfica sem especificar o elipsoide usado. Muitos mapas mantidos por agências nacionais s?o baseados em elipsoides mais antigos, ent?o é necessário saber como os valores de latitude e longitude s?o transformados de um elipsoide para outro. Dispositivos GPS incluem software para realizar transforma??es de datum que ligam o WGS84 ao elipsoide de referência local com sua grade associada.

A geometria do elipsoide

Uma esfera de raio a comprimida ao longo do eixo z para formar um elipsoide oblato de revolu??o.

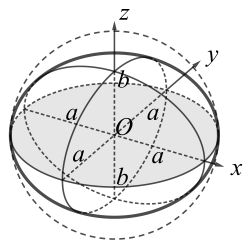
A forma de um elipsoide de revolu??o é determinada pela forma da elipse que é rotacionada ao redor de seu eixo menor (mais curto). S?o necessários dois parametros. Um é invariavelmente o raio equatorial, que é o semi-eixo maior, a. O outro parametro é geralmente (1) o raio polar ou semi-eixo menor, b; ou (2) o achatamento (primeiro), f; ou (3) a excentricidade, e. Esses parametros n?o s?o independentes: eles est?o relacionados por

$f={\frac {a-b}{a}},\qquad e^{2}=2f-f^{2},\qquad b=a(1-f)=a{\sqrt {1-e^{2}}}\,.$

Muitos outros parametros (veja elipse, elipsoide) aparecem no estudo da geodesia, geofísica e proje??es de mapas, mas todos podem ser expressos em termos de um ou dois membros do conjunto a, b, f e e. Tanto f quanto e s?o pequenos e frequentemente aparecem em expans?es em série em cálculos; eles s?o da ordem de ⁠1/298⁠ e 0,0818, respectivamente. Valores para vários elipsoides s?o fornecidos em Forma da Terra. Os elipsoides de referência s?o geralmente definidos pelo semi-eixo maior e pelo achatamento inverso, ⁠1/f⁠. Por exemplo, os valores de defini??o para o elipsoide WGS84, usado por todos os dispositivos GPS, s?o

• a (raio equatorial): 63 78 137,0 m exatamente
• ⁠1/f⁠ (achatamento inverso): 298,257223563 exatamente

dos quais s?o derivados

• b (raio polar): 6356752,31425 m
• e² (excentricidade ao quadrado): 0,006 694 379 990 14

A diferen?a entre os semi-eixos maior e menor é cerca de 21 km e como fra??o do semi-eixo maior, é igual ao achatamento; em um monitor de computador, o elipsoide poderia ser dimensionado como 300 por 299 pixels. Isso mal seria distinguível de uma esfera de 300 por 300 pixels, ent?o as ilustra??es geralmente exageram o achatamento.

Latitudes geodésica e geocêntrica

A defini??o de latitude geodésica ($\phi$) e longitude ($\lambda$) em um elipsoide. A normal à superfície n?o passa pelo centro, exceto no equador e nos polos.

A grade no elipsoide é construída exatamente da mesma forma que na esfera. A normal em um ponto na superfície de um elipsoide n?o passa pelo centro, exceto para pontos no equador ou nos polos, mas a defini??o de latitude permanece inalterada como o angulo entre a normal e o plano equatorial. A terminologia para latitude deve ser tornada mais precisa distinguindo:

• Latitude geodésica: o angulo entre a normal e o plano equatorial. A nota??o padr?o em publica??es em inglês é ?. Esta é a defini??o assumida quando a palavra latitude é usada sem qualifica??o. A defini??o deve ser acompanhada por uma especifica??o do elipsoide.
• Latitude geocêntrica (também conhecida como latitude esférica, após o ?ngulo polar 3D): o angulo entre o raio (do centro ao ponto na superfície) e o plano equatorial. (Figura abaixo). N?o há nota??o padr?o: exemplos de vários textos incluem θ, ψ, q, ?′, ?_c, ?_g. Este artigo usa θ.

Latitude geográfica deve ser usada com cuidado, pois alguns autores a usam como sin?nimo de latitude geodésica, enquanto outros a usam como alternativa à latitude astron?mica. "Latitude" (n?o qualificada) deve normalmente se referir à latitude geodésica.

A importancia de especificar o datum de referência pode ser ilustrada por um exemplo simples. No elipsoide de referência para WGS84, o centro da Torre Eiffel tem uma latitude geodésica de 48° 51′ 29″ N, ou 48.8583° N e longitude de 2° 17′ 40″ E ou 2.2944°E. As mesmas coordenadas no datum ED50 definem um ponto no solo que está 140 metres (460 feet) distante da torre.^{[carece de fontes]} Uma busca na web pode produzir vários valores diferentes para a latitude da torre; o elipsoide de referência raramente é especificado.

Distancia do meridiano

Ver artigo principal: Arco de meridiano

O comprimento de um grau de latitude depende da forma da Terra assumida.

Distancia do meridiano na esfera

Na esfera, a normal passa pelo centro e a latitude (?) é portanto igual ao angulo subtendido no centro pelo arco do meridiano do equador até o ponto em quest?o. Se a distancia do meridiano for denotada por m(?) ent?o

$m(\phi )={\frac {\pi }{180^{\circ }}}R\phi _{\mathrm {graus} }=R\phi _{\mathrm {radianos} }$

onde R denota o raio médio da Terra. R é igual a 6 371 km ou 3 959 milhas. Nenhuma precis?o mais alta é apropriada para R, pois resultados de maior precis?o exigem um modelo elipsoide. Com este valor para R, o comprimento do meridiano de 1 grau de latitude na esfera é de 111,2 km (69,1 milhas estatutárias) (60,0 milhas náuticas). O comprimento de 1 minuto de latitude é de 1 853 km (1 151 milhas estatutárias) (1,00 milhas náuticas), enquanto o comprimento de 1 segundo de latitude é de 30,8 m ou 101 pés (veja milha náutica).

Distancia do meridiano no elipsoide

Em Arco de meridiano e textos padr?o é mostrado que a distancia ao longo de um meridiano da latitude ? até o equador é dada por (? em radianos)

$m(\phi )=\int _{0}^{\phi }M(\phi ')\,d\phi '=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '$

onde M(?) é o raio de curvatura meridional.

A distancia do meridiano de um quarto do equador até o polo é

$m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,$

Para WGS84 esta distancia é 10 001,965 729 km.

A avalia??o da integral da distancia do meridiano é central para muitos estudos em geodesia e proje??o de mapas. Ela pode ser avaliada expandindo a integral pela série binomial e integrando termo por termo: veja Arco de meridiano para detalhes. O comprimento do arco do meridiano entre duas latitudes dadas é obtido substituindo os limites da integral pelas latitudes em quest?o. O comprimento de um pequeno arco de meridiano é dado por

$\delta m(\phi )=M(\phi )\,\delta \phi =a\left(1-e^{2}\right)\left(1-e^{2}\sin ^{2}\phi \right)^{-{\frac {3}{2}}}\,\delta \phi$

$\phi$	Δ1 lat	Δ1 long
0°	110,574 km	111,320 km
15°	110,649 km	107,550 km
30°	110,852 km	96,486 km
45°	111,132 km	78,847 km
60°	111,412 km	55,800 km
75°	111,618 km	28,902 km
90°	111,694 km	0,000 km

Quando a diferen?a de latitude é de 1 grau, correspondente a ⁠π/180⁠ radianos, a distancia do arco é de aproximadamente

$\Delta _{\text{lat}}^{1}={\frac {\pi a\left(1-e^{2}\right)}{180^{\circ }\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {3}{2}}}}$

A distancia em metros (correta até 0,01 metro) entre as latitudes $\phi$ ? 0,5 graus e $\phi$ + 0,5 graus no elipsoide WGS84 é

$\Delta _{\text{lat}}^{1}=111\ 132,954-559,822\cos 2\phi +1,175\cos 4\phi$

A varia??o dessa distancia com a latitude (no WGS84) é mostrada na tabela juntamente com o comprimento de um grau de longitude (distancia leste-oeste):

$\Delta _{\text{long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {1-e^{2}\sin ^{2}\phi }}}}\,$

Uma calculadora para qualquer latitude é fornecida pela Agência Nacional de Inteligência Geoespacial (NGA) do governo dos EUA.

O gráfico a seguir ilustra a varia??o de um grau de latitude e de um grau de longitude com a latitude.

A defini??o de latitude geodésica (?) e latitude geocêntrica (θ).

Latitudes auxiliares

Existem seis latitudes auxiliares que têm aplica??es para problemas especiais em geodesia, geofísica e teoria de proje??es de mapas:

• Latitude geocêntrica
• Latitude paramétrica (ou latitude reduzida)
• Latitude retificadora
• Latitude autálica
• Latitude conforme
• Latitude isométrica

As defini??es dadas nesta se??o relacionam-se a locais na superfície de referência elipsoidal, mas as duas primeiras latitudes auxiliares, como a latitude geodésica, podem ser estendidas para definir um sistema de coordenadas geográficas tridimensional, como discutido abaixo. As demais latitudes n?o s?o usadas dessa forma; s?o usadas apenas como constru??es intermediárias em proje??es de mapas do elipsoide de referência para o plano ou em cálculos de geodésicas no elipsoide. Seus valores numéricos n?o s?o de interesse. Por exemplo, ninguém precisaria calcular a latitude autálica da Torre Eiffel.

As express?es abaixo fornecem as latitudes auxiliares em termos da latitude geodésica, do semi-eixo maior, a, e da excentricidade, e. (Para inversos, veja abaixo.) As formas fornecidas s?o, exceto variantes notacionais, aquelas na referência padr?o para proje??es de mapas, a saber "Map projections: a working manual" de J. P. Snyder. Deriva??es dessas express?es podem ser encontradas em Adams e publica??es online de Osborne e Rapp.

Latitude geocêntrica

Ver também: § Latitudes geodésica e geocêntrica

A defini??o de latitude geodésica (?) e latitude geocêntrica (θ)

A latitude geocêntrica é o angulo entre o plano equatorial e o raio do centro para um ponto de interesse.

Quando o ponto está na superfície do elipsoide, a rela??o entre a latitude geocêntrica (θ) e a latitude geodésica (?) é:

$\theta (\phi )=\tan ^{-1}\left(\left(1-e^{2}\right)\tan \phi \right)=\tan ^{-1}\left((1-f)^{2}\tan \phi \right)\,.$

Para pontos que n?o est?o na superfície do elipsoide, o relacionamento envolve adicionalmente a altura elipsoidal h:

$\theta (\phi ,h)=\tan ^{-1}\left({\frac {N(1-f)^{2}+h}{N+h}}\tan \phi \right)$

onde N é o raio de curvatura do primeiro vertical. As latitudes geodésica e geocêntrica s?o iguais no equador e nos polos, mas em outras latitudes elas diferem por alguns minutos de arco. Tomando o valor da excentricidade ao quadrado como 0,0067 (depende da escolha do elipsoide), pode-se mostrar que a diferen?a máxima de $\phi {-}\theta$ é de cerca de 11,5 minutos de arco a uma latitude geodésica de aproximadamente 45° 6′.

Latitude paramétrica (ou reduzida)

Defini??o da latitude paramétrica (β) no elipsoide

A latitude paramétrica ou latitude reduzida, β, é definida pelo raio desenhado do centro do elipsoide até aquele ponto Q na esfera circundante (de raio a) que é a proje??o paralela ao eixo da Terra de um ponto P no elipsoide na latitude ?. Foi introduzida por Legendre e Bessel que resolveram problemas para geodésicas no elipsoide transformando-os em um problema equivalente para geodésicas esféricas usando esta latitude menor. A nota??o de Bessel, u(?), também é usada na literatura atual. A latitude paramétrica está relacionada à latitude geodésica por:

$\beta (\phi )=\tan ^{-1}\left({\sqrt {1-e^{2}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)$

O nome alternativo surge da parametriza??o da equa??o da elipse descrevendo uma se??o meridiana. Em termos de coordenadas cartesianas p, a distancia do eixo menor, e z, a distancia acima do plano equatorial, a equa??o da elipse é:

${\frac {p^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1\,.$

As coordenadas cartesianas do ponto s?o parametrizadas por

$p=a\cos \beta \,,\qquad z=b\sin \beta \,;$

Cayley sugeriu o termo latitude paramétrica por causa da forma dessas equa??es.

A latitude paramétrica n?o é usada na teoria das proje??es de mapas. Sua aplica??o mais importante é na teoria das geodésicas elipsoidais, (Vincenty, Karney).

Latitude retificadora

A latitude retificadora, μ, é a distancia do meridiano escalonada de modo que seu valor nos polos seja igual a 90 graus ou ⁠π/2⁠ radianos:

$\mu (\phi )={\frac {\pi }{2}}{\frac {m(\phi )}{m_{\mathrm {p} }}}$

onde a distancia do meridiano do equador até uma latitude ? é (veja Arco de meridiano)

$m(\phi )=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '\,,$

e o comprimento do quadrante do meridiano do equador ao polo (a distancia polar) é

$m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,.$

Usar a latitude retificadora para definir uma latitude em uma esfera de raio

$R={\frac {2m_{\mathrm {p} }}{\pi }}$

define uma proje??o do elipsoide para a esfera de modo que todos os meridianos tenham comprimento verdadeiro e escala uniforme. A esfera pode ent?o ser projetada para o plano com uma proje??o equirretangular para dar uma proje??o dupla do elipsoide para o plano, de modo que todos os meridianos tenham comprimento verdadeiro e escala meridiana uniforme. Um exemplo do uso da latitude retificadora é a proje??o c?nica equidistante. (Snyder, Se??o 16). A latitude retificadora também é de grande importancia na constru??o da Proje??o de Mercator Transversa.

Latitude autálica

Ver também: Raio autálico

A latitude autálica (do grego para "mesma área"), ξ, fornece uma proje??o de área igual para uma esfera.

$\xi (\phi )=\sin ^{-1}\left({\frac {q(\phi )}{q_{\mathrm {p} }}}\right)$

onde

${\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)\\[2pt]&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}+{\frac {1-e^{2}}{e}}\tanh ^{-1}(e\sin \phi )\end{aligned}}$

e

${\begin{aligned}q_{\mathrm {p} }=q\left({\frac {\pi }{2}}\right)&=1-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e}{1+e}}\right)\\&=1+{\frac {1-e^{2}}{e}}\tanh ^{-1}e\end{aligned}}$

e o raio da esfera é tomado como

$R_{q}=a{\sqrt {\frac {q_{\mathrm {p} }}{2}}}\,.$

Um exemplo do uso da latitude autálica é a proje??o c?nica de Albers de área igual.

Latitude conforme

A latitude conforme, χ, fornece uma transforma??o que preserva o angulo (conforme) para a esfera.

${\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {1+\sin \phi }{1-\sin \phi }}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{e}\right]^{\frac {1}{2}}-{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{\frac {e}{2}}\right]-{\frac {\pi }{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\operatorname {gd} \left[\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi )\right]\end{aligned}}$

onde gd(x) é a Fun??o Gudermanniana. (Veja também Proje??o de Mercator.)

A latitude conforme define uma transforma??o do elipsoide para uma esfera de raio arbitrário de modo que o angulo de interse??o entre quaisquer duas linhas no elipsoide seja o mesmo que o angulo correspondente na esfera (de modo que a forma de pequenos elementos seja bem preservada). Uma nova transforma??o conforme da esfera para o plano dá uma proje??o conforme dupla do elipsoide para o plano. Esta n?o é a única forma de gerar tal proje??o conforme. Por exemplo, a vers?o 'exata' da Proje??o de Mercator Transversa no elipsoide n?o é uma proje??o dupla. (Ela envolve, no entanto, uma generaliza??o da latitude conforme para o plano complexo).

Latitude isométrica

A latitude isométrica, ψ, é usada no desenvolvimento das vers?es elipsoidais da Proje??o de Mercator normal e da Proje??o de Mercator Transversa. O nome "isométrica" surge do fato de que em qualquer ponto do elipsoide, incrementos iguais de ψ e longitude λ d?o origem a deslocamentos de distancia iguais ao longo dos meridianos e paralelos, respectivamente. A grade definida pelas linhas de constante ψ e constante λ, divide a superfície do elipsoide em uma malha de quadrados (de tamanho variável). A latitude isométrica é zero no equador, mas diverge rapidamente da latitude geodésica, tendendo ao infinito nos polos. A nota??o convencional é dada em Snyder (página 15):

${\begin{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}}\right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\&=\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi ).\end{aligned}}$

Para a normal Proje??o de Mercator (no elipsoide), esta fun??o define o espa?amento dos paralelos: se o comprimento do equador na proje??o é E (unidades de comprimento ou pixels), ent?o a distancia, y, de um paralelo de latitude ? do equador é

$y(\phi )={\frac {E}{2\pi }}\psi (\phi )\,.$

A latitude isométrica ψ está intimamente relacionada à latitude conforme χ:

$\psi (\phi )=\operatorname {gd} ^{-1}\chi (\phi )\,.$

Fórmulas inversas e séries

As fórmulas nas se??es anteriores fornecem a latitude auxiliar em termos da latitude geodésica. As express?es para as latitudes geocêntrica e paramétrica podem ser invertidas diretamente, mas isso é impossível nos quatro casos restantes: as latitudes retificadora, autálica, conforme e isométrica. Existem dois métodos para prosseguir.

• O primeiro é uma invers?o numérica da equa??o de defini??o para cada valor particular da latitude auxiliar. Os métodos disponíveis s?o itera??o de ponto fixo e Newton–Raphson para encontrar raízes.
  • Ao converter de isométrica ou conforme para geodésica, duas itera??es de Newton-Raphson fornecem precis?o dupla precis?o.
• A outra abordagem, mais útil, é expressar a latitude auxiliar como uma série em termos da latitude geodésica e, em seguida, inverter a série pelo método da Revers?o de Lagrange. Tais séries s?o apresentadas por Adams, que usa expans?es em séries de Taylor e fornece coeficientes em termos da excentricidade. Orihuela fornece séries para as convers?es entre todos os pares de latitudes auxiliares em termos do terceiro achatamento, n = (a - b)/(a + b). Karney estabelece que os erros de truncamento para tais séries s?o consistentemente menores que as séries equivalentes em termos da excentricidade. O método de séries n?o é aplicável à latitude isométrica e deve-se encontrar a latitude conforme em um passo intermediário.

Compara??o numérica de latitudes auxiliares

inline

O gráfico à direita mostra a diferen?a entre a latitude geodésica e as latitudes auxiliares, exceto a latitude isométrica (que diverge ao infinito nos polos), para o caso do elipsoide WGS84. As diferen?as mostradas no gráfico est?o em minutos de arco. No hemisfério norte (latitudes positivas), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ?; no hemisfério sul (latitudes negativas), as desigualdades s?o invertidas, com igualdade no equador e nos polos. Embora o gráfico pare?a simétrico em torno de 45°, os mínimos das curvas na verdade se situam entre 45° 2′ e 45° 6′. Alguns pontos de dados representativos s?o fornecidos na tabela abaixo. As latitudes conforme e geocêntrica s?o praticamente indistinguíveis, fato que foi explorado nos dias dos cálculos manuais para agilizar a constru??o de proje??es de mapas.

Na primeira ordem no achatamento f, as latitudes auxiliares podem ser expressas como ζ = ? ? Cf sin 2? onde a constante C assume os valores [1⁄2, 2⁄3, 3⁄4, 1, 1] para ζ = [β, ξ, μ, χ, θ].

Diferen?a aproximada da latitude geodésica (?)

?	Paramétrica β ? ?	Autálica ξ ? ?	Retificadora μ ? ?	Conforme χ ? ?	Geocêntrica θ ? ?
0°	0,00′	0,00′	0,00′	0,00′	0,00′
15°	?2.88′	?3,84′	?4,32′	?5,76′	?5,76′
30°	?5,00′	?6,66′	?7,49′	?9,98′	?9,98′
45°	?5,77′	?7,70′	?8,66′	?11,54′	?11,55′
60°	?5,00′	?6,67′	?7,51′	?10,01′	?10,02′
75°	?2,89′	?3,86′	?4,34′	?5,78′	?5,79′
90°	0,00′	0,00′	0,00′	0,00′	0,00′

Latitude e sistemas de coordenadas

A latitude geodésica, ou qualquer uma das latitudes auxiliares definidas no elipsoide de referência, constitui com a longitude um sistema de coordenadas bidimensional nesse elipsoide. Para definir a posi??o de um ponto arbitrário é necessário estender tal sistema de coordenadas para três dimens?es. Três latitudes s?o usadas desta forma: as latitudes geodésica, geocêntrica e paramétrica s?o usadas em coordenadas geodésicas, coordenadas polares esféricas e coordenadas elipsoidais, respectivamente.

Coordenadas geodésicas

Ver artigo principal: Coordenadas geodésicas

Coordenadas geodésicas P(?,λ,h)

Em um ponto arbitrário P, considere a linha PN que é normal ao elipsoide de referência. As coordenadas geodésicas P(?,λ,h) s?o a latitude e longitude do ponto N no elipsoide e a distancia PN. Essa altura difere da altura acima do geoide ou de uma altura de referência, como a altura acima do nível médio do mar em um local específico. A dire??o de PN também diferirá da dire??o de uma linha vertical de prumo. A rela??o dessas diferentes alturas requer conhecimento da forma do geoide e também do campo gravitacional da Terra.

Coordenadas polares esféricas

Coordenada geocêntrica relacionada às coordenadas polares esféricas P(r,θ′,λ)

A latitude geocêntrica θ é o complemento do angulo polar ou colatitude θ′ nas coordenadas polares esféricas convencionais nas quais as coordenadas de um ponto s?o P(r,θ′,λ) onde r é a distancia de P do centro O, θ′ é o angulo entre o vetor radial e o eixo polar e λ é a longitude. Como a normal em um ponto geral no elipsoide n?o passa pelo centro, é claro que os pontos P' na normal, que têm todos a mesma latitude geodésica, ter?o latitudes geocêntricas diferentes. Sistemas de coordenadas polares esféricas s?o usados na análise do campo gravitacional.

Coordenadas harm?nicas elipsoidais

Coordenadas elipsoidais P(u,β,λ)

A latitude paramétrica também pode ser estendida para um sistema de coordenadas tridimensional. Para um ponto P que n?o está no elipsoide de referência (semieixos OA e OB), construa um elipsoide auxiliar que seja confocal (mesmos focos F, F′) com o elipsoide de referência: a condi??o necessária é que o produto ae do semieixo maior e da excentricidade seja o mesmo para ambos os elipsoides. Seja u o semi-eixo menor (OD) do elipsoide auxiliar. Além disso, seja β a latitude paramétrica de P no elipsoide auxiliar. O conjunto (u,β,λ) define as coordenadas harm?nicas elipsoidais ou simplesmente coordenadas elipsoidais (embora esse termo também seja usado para se referir à coordenada geodésica). Essas coordenadas s?o a escolha natural em modelos do campo gravitacional para um corpo elipsoidal em rota??o. O acima se aplica a um elipsoide biaxial (um esferoide, como em coordenadas esferoidais oblatas); para uma generaliza??o, veja coordenadas elipsoidais triaxiais.

Convers?es de coordenadas

As rela??es entre os sistemas de coordenadas acima e também as coordenadas cartesianas n?o s?o apresentadas aqui. A transforma??o entre coordenadas geodésicas e cartesianas pode ser encontrada em convers?o de coordenadas geográficas. A rela??o entre coordenadas cartesianas e polares esféricas é dada em sistema de coordenadas esféricas. A rela??o entre coordenadas cartesianas e elipsoidais é discutida em Torge.

Latitude astron?mica

1. Oceano
2. Elipsoide
3. Linha de prumo local
4. Continente
5. Geóide

Latitude astron?mica (Φ) é o angulo entre o plano equatorial e a verdadeira dire??o vertical em um ponto na superfície. A verdadeira vertical, a dire??o de uma linha de prumo, é também a dire??o da gravidade (o resultado da acelera??o gravitacional (baseada em massa) e da acelera??o centrífuga) nessa latitude. A latitude astron?mica é calculada a partir de angulos medidos entre o zênite e estrelas cuja declina??o é conhecida com precis?o.

Em geral, a verdadeira vertical em um ponto na superfície n?o coincide exatamente com a normal ao elipsoide de referência ou com a normal ao geoide. O geoide é uma forma idealizada e teórica "ao nível médio do mar". Pontos em terra n?o est?o exatamente no geoide, e a vertical em um ponto em um momento específico é influenciada por for?as de maré que o geoide teórico média. O angulo entre as normais astron?mica e geodésica é chamado de desvio vertical e geralmente é de alguns segundos de arco, mas é importante na geodesia.

A latitude astron?mica n?o deve ser confundida com declina??o, a coordenada que os astr?nomos usam de maneira semelhante para especificar a posi??o angular das estrelas ao norte-sul do equador celestial (veja coordenadas equatoriais), nem com latitude da eclíptica, a coordenada que os astr?nomos usam para especificar a posi??o angular das estrelas ao norte-sul da eclíptica (veja coordenadas eclípticas).

Ver também

• Altitude (nível médio do mar)
• Bowditch's American Practical Navigator
• Dire??o cardeal
• Círculo de latitude
• Colatitude
• Declina??o na esfera celeste
• Projeto de Confluência de Graus
• Geodesia
• Datum geodésico
• Sistema de coordenadas geográficas
• Distancia geográfica
• Latitude geomagnética
• Geotagging
• Distancia de círculo máximo
• História da latitude
• Latitudes dos cavalos
• Servi?o Internacional de Latitude
• Lista de países por latitude
• Longitude
• Código de área Natural
• Navega??o
• Ordem de grandeza (comprimento)
• Sistema Geodésico Mundial

Liga??es externas

• Servidor de Nomes GEONets. Arquivado em 2025-08-14 no Wayback Machine. acesso ao banco de dados de nomes de características geográficas estrangeiras da National Geospatial-Intelligence Agency (NGA).
• Recursos para determinar sua latitude e longitude Arquivado em 2025-08-14 no Wayback Machine
• Converter graus decimais em graus, minutos, segundos
• Cálculo de distancia com base em latitude e longitude – vers?o em JavaScript
• Levantamento de Latitude do Século XVI
• Determina??o de Latitude por Francis Drake na Costa da Califórnia em 1579